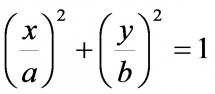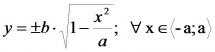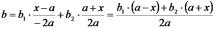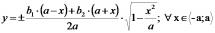Rovnice vajíčka - jednoduchá jako Kolumbovo vejce :-)
Jirka Landa 29.3.-23.4.2013
V poslední době proběhly tiskem články o tom, že není známá rovnice popisující tvar vejce (např. ihned.cz, novinky.cz, iprima.cz). Nikdy před tím jsem nad tvarem vejce z matematického hlediska nepřemýšlel, až do přečtení těchto článků. Napadlo mě následující řešení: Každá ze špiček vajíčka, tedy tupá i ostrá připomíná rotační elipsoid. Je tedy možné, že jde o dva elipsoidy, které plynule přecházejí jeden do druhého. Zkusil jsem tedy takovouto křivku naprogramovat pomocí SW Scilab. Výsledek předčil očekávání. Zdá se, že tímto vznikne univerzální parametrická rovnice vejce, která je schopná zobrazit různé tvary vajec od kulových až po protáhle elipsovité. Navíc je možné tuto rovnici dále rozvíjet.
Odvození rovnice:
Vyjdeme z rovnice elipsy (1) (podle wikipedia.org):
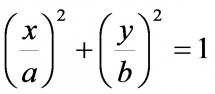
Popisek
(1)
Rovnici (1) upravíme do tvaru:
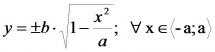
Popisek
(2)
Dále předpokládáme, že obě elipsy mají stejnou poloosu a, tedy a1=a2=a, ale obecně různé poloosy b, tedy b1≠b2. Váha parametru b1 se mění od 1 v bodě x=-a do 0 v bodě x=a, a opačně váha parametru b2 je v bodě x=-a 0 a postupně roste na 1 v bodě x=a. Do rovnice (2) tedy za parametr poloosy b dosadíme vážený průměr hodnot b1 a b2, viz rovnice (3)
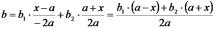
Popisek
(3)
Celková rovnice obvodové křivky vajíčka je tedy (4):
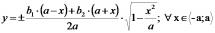
Popisek
(4)
Výsledné zobrazení:
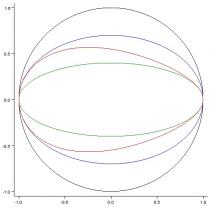
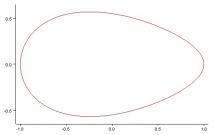
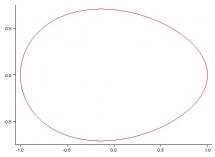
Na Obr. 1 je porovnání kružnice (černě) o poloměru a (to je z důvodu možného zkreslení obrázku při zobrazení na monitoru či při tisku), modrá je elipsa 1, zelená elipsa 2 a výsledné vajíčko je červeně. Na Obr. 2 a Obr. 3 jsou pak zobrazeny čisté křivky vajíček pro různé hodnoty parametrů b1 a b2.
Popisek
OBR. 1: porovnání původních elips a křivky vajíčka (červeně), kde a=1 (černá kružnice), b1=0.7 (modrá elipsa) a b2=0.4 (zelená elipsa).
Popisek
Obr. 2: křivka vajíčka, pro a=1, b1=0.7 a b2=0.4.
Popisek
Obr. 3: křivka vajíčka, pro a=1, b1=0.8 a b2=0.6.
Závěr
Závěrem lze říci, že rovnice (4) dobře popisuje tvary různých vajec, které jsou určeny pomocí parametrů a, b1 a b2. Rovnici určující parametr b (3), lze zřejmě podle potřeby zvolit i jinak, ale výsledné křivky se zdají být dobré i podle tohoto tvaru.
názory k článku
to je lol :D - 23.10.2013 18:38
:D
Poznámka
Ve společnosti s možností svobodného uplatnění a přijetí přinejmenším věrohodného názoru, by desková tektonika na základě jenom jediného z uvedených 23 článků o pochybeních už dávno skončila v archivu neplatných teorií. Její udržování a neustálá další propagace jsou důkazem ovlivňování vědeckého výzkumu politickými prostředky. Z tohoto důvodu jsme zařadili na stránky i články k této problematice, viz článek Michiheiho Hoshiny, jeho dodatek a článek ropný zlom v kapitole o rozpínání Země.
Velké východojaponské zemětřesení otřáslo (také) deskovou tektonikou
Yoshihiro KUBOTA, Niigata University, Japan: „SYMPOZIUM K PŘÍLEŽITOSTI 20. VÝROČÍ ROZPRAV O STRUKTURNÍ GEOLOGII; 18. PROSINCE 2011 JAPONSKO. Strukturně geologická kolokvia byla zavedena v roce 1991. Od té doby jsme zorganizovali pravidelně dvakrát ročně schůze za účelem podpory původních výzkumů založených na důkladných terénních pracích… Japonci se obávají dalšího velkého zemětřesení... Výsledek sympozia byl překvapující. Všichni účastníci (více jak 50), nabyli silného neodbytného pocitu, že éra deskové tektoniky skončila a velká zemětřesení jsou jistě předvídatelná."
NCGT: New Concepts in Global Tectonics NEWSLETTER No. 61, December, 2011 ISSN: 1833-2560 Editor: Dong R. CHOI

Popisek
Na obr. Dong Choi přednáší o velkém Japonském zemětřesení
Pozn. autora webu: Závěr z diskuse v Japonsku je jasný: nejen z hlediska předpovídání zemětřesení nelze brát deskovou tektoniku vážně a je tudíž z hlediska předpovídání zemětřesení naprosto nepoužitelná (i když odjakživa tvrdila, že "vysvětluje zemětřesení").